What is Ray Tracing?
Ray tracing, as explained by Glassner[1], is an ensemble of computational and mathematical techniques used to produce a 2-D picture of 3-D elements. It is based, in principle, on a simple camera model called the pinhole camera, a box containing photographic film and a very small opening on the opposite side, letting only certain rays of light to come in contact with the film, thus printing a focused image on it. The ray tracer uses a variation of this pinhole camera called a frustum which we will look at below.
Ray tracing could be considered a simulation of natural light reflection; Natural light bounces off objects in all directions but only the rays entering the eye are visible. A ray tracer, as it is incapable of dealing with an infinity of light rays, will only deal with rays that follow the path from the light source to the eye. Perhaps the most important aspect of ray tracer lies in this particular ray-eye relationship, where of instead of plotting the trajectory of a ray of light from its source to eye, we reverse the process, and plot a ray from the eye to the light source, knowing that if this ray reaches the light source it must be visible to the eye and therefore used in the rendering process. This concept enables us to eliminate dealing with stray light rays. This is referred to as backwards ray tracing as opposed to forward ray tracing, which is closest to reality, but much more difficult to implement.
Ray tracing, as explained by Glassner[1], is an ensemble of computational and mathematical techniques used to produce a 2-D picture of 3-D elements. It is based, in principle, on a simple camera model called the pinhole camera, a box containing photographic film and a very small opening on the opposite side, letting only certain rays of light to come in contact with the film, thus printing a focused image on it. The ray tracer uses a variation of this pinhole camera called a frustum which we will look at below.
Ray tracing could be considered a simulation of natural light reflection; Natural light bounces off objects in all directions but only the rays entering the eye are visible. A ray tracer, as it is incapable of dealing with an infinity of light rays, will only deal with rays that follow the path from the light source to the eye. Perhaps the most important aspect of ray tracer lies in this particular ray-eye relationship, where of instead of plotting the trajectory of a ray of light from its source to eye, we reverse the process, and plot a ray from the eye to the light source, knowing that if this ray reaches the light source it must be visible to the eye and therefore used in the rendering process. This concept enables us to eliminate dealing with stray light rays. This is referred to as backwards ray tracing as opposed to forward ray tracing, which is closest to reality, but much more difficult to implement.
The pinhole camera
 |
| Pinhole camera principle (image courtesy of Wikipedia) |
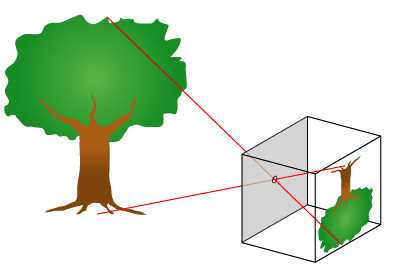
The frustum: a modified pinhole camera used in computer graphics
 |
| Viewing frustum, a modified pinhole camera. (Illustration by Martin Bertrand) The modified pinhole camera has the eye (or the viewpoint) separated from the object by the viewing window. This window, in our implementation, can be built as an image buffer (or frame buffer) Only objects contained inside an imaginary space of the shape of a truncated pyramid will be visible. The viewing window would be the truncated top part of this pyramid, and the viewpoint the top. This truncated pyramid is called a frustum. The frustum, we must note, does not have a base as the pyramid's sides extend to infinity. Any object inscribed inside the frustum's volume should be visible, unless hidden by another object. The image pixel and the ray It is at the intersection of the viewing window and the ray that the actual rendering process will be located; When the ray passes through the viewing window on its way to the object, its position in the window can easily be found. If we then calculate the correct light intensity at that point, doing so for all points available in viewing window should create a viewable image. Once an intensity value has been established, it is also easy to assign this value to a screen pixel, thus enabling us to see the image onscreen. |
 |
| Viewing window with image of object (Image courtesy of Wikipedia) |
The viewing window and the image buffer
The first critical element that we can implement in our program is the viewing window: The java interface for the Simple Ray Tracer program consists of a simple GUI that can display an image of fixed dimensions: 500 pixels wide by 400 pixels high.
 |
| The Simple Ray Tracer GUI showing an empty 500 by 400 pixel viewing window. The program uses a BufferedImage image object embedded in a JLabel component. Each pixel of the image can easily be changed by modifying its RGB value by first creating a Colour object with separate integer values ranging from 0 to 255 and then inserting this colour value, which will represent the light intensity, at a specific X Y coordinate. There is also a fourth pixel parameter, A, which controls transparency. It is not used in the application and is permanently set to 1. Here is the application's code snippet for setting a given pixel's intensity: Color col = new Color((int)average_intensity[0],(int) average_intensity[1],(int)average_intensity[2],1); raytracer.screen_array.setRGB(buff_z, buff_y, col.getRGB()); |
The average_intensity is a size 3 double type array for RGB values which are computed separately. The values are cast for Integer before creating the colour object. The colour object built is then sent to the GUI's screen array which sets the pixel's intensity at the Z and Y coordinates (here called buff_z and buff_y). Z and Y coordinates were used instead of X and Y for practical purposes as the in-world viewing window was built parallel to the Y Z plane. The details of the world coordinates are briefly explained below.
Objects in an abstract frame of reference: 3-D vector coordinates
Objects in an abstract frame of reference: 3-D vector coordinates
This viewing window / viewpoint / object relationship can best be implemented with an object oriented approach: By defining each element as a specific object with its methods and data members, new elements can easily be added to progressively build a more complex scene. Any object oriented language would be appropriate for the task at hand, but in this particular case the language of choice has been Java.
The objects created must interact with each other within an outside frame of reference: for example, the viewpoint must be at a certain distance from the viewing window and any object behind the window will appear to be larger or smaller depending on its distance from the window. These distances must be quantified in any ray-tracing application. One possible solution would be to build a world object as a 3 dimensional array, where the array's indices would correspond to the coordinates of the objects contained in the world. Although feasible, this method would be complex and difficult to modify. A much simpler solution is giving each created object 3 dimensional coordinates building blocks, in the form of vectors expressed as [x,y,z].
For example, a viewpoint object could have a coordinate defined by the vector [0, 0, 0] and a sphere to be rendered could have a center located at [10, 23, 11] with a radius of 2. A triangular polygon object, the simplest polygon object possible, could be defined as a trio of 3D vectors, one for each vertice of the polygon. Other object attributes could easily be added like ambient colour for instance.
Linear algebra concepts: Implicit equations
The viewing window, like other objects with multiple vertices in the world, are implicitly defined by the vertices that compose them. They are not entities that occupy actual memory space, they are simply referred to by their initialized vertice data members. Their implicit nature is in fact, critical for certain algorithms that are used. For instance, a plane object, necessary for the rendering of polygons is implicitly defined with the formula
Ax + By + Cz + D = 0
Where ABC are the x y z values of the normal vector to this plane, and D being the distance of the plane from the world's origin defined as [0,0,0].
Points that are included in the plane are considered implicit by the fact that if a point fits in the equation it is considered part of the plane. The same concept also applies to spheres: Here, a sphere is defined as a set of points that satisfy the following equation
(Xs - Xc)2 + (Ys - Yc)2 + (Zs - Zc)2 = S2r
Where the sphere's surface is the set of points [Xs, Ys, Zs], the sphere's centre is
[Xc, Yc, Zc] and sphere's radius is Sr. We will come back to these equations as we will use them equation to render our objects.
Basic objects and coordinate values used in the Simple Ray Tracer application
Main class : RayTracer class
This is the main class of the program: Apart from creating the GUI components, (The image buffer and its window) it contains the main(String[] args) method, where objects and light sources to be rendered in the scene are created, but also where the other important class is instantiated, the ViewPoint class.
ViewPoint class:
The viewPoint class creates a viewpoint object, and a viewing window object. Here, our viewpoint (henceforth VP) will have a coordinate of [0, 2, 2.5]. Our viewing window, defined by 4 points is a rectangular polygon set on a plane parallel to the Y Z coordinates as mentioned earlier. The bottom left corner is established at [10, 0, 0] while the top right corner is located at [10, 4, 5] in world coordinates. It is useful to notice that the rectangle can be defined by these 2 points. The other points were simply added as a visual guide. The coordinates of the viewpoint place it in exactly in the center of the viewing window. This will facilitate approximating values as the X component of vector lengths between viewpoint and viewing window will be of value 10.
Here is a diagram of the location of the principal elements of the ray tracer
 |
| Principal elements coordinates of the Simple Ray Tracer application (Illustration by Martin Bertrand) |
Inner world coordinates vs outside world coordinates
It is interesting to notice that even thought the image has a 500 by 400 size, our viewing window possesses a 5 by 4 size, expressed in world units. World units here are simply Cartesian values; they have no direct relation with the outside world. They are self contained. To match our pixel screen's position to the viewing window we will simply divide the worlds coordinates by 100. We will look at this later in more detail when we will calculate unit vectors.
VisibleObject class:
The VisibleObject class is an abstract super class from which the Sphere and Polygon class are derived. The VisibleObject class contains a center data member that can contain the center coordinate of a sphere instance. This abstract class also contains other data members, but those being related to object luminosity, colour and reflexive capabilities, these members will be best explained in the Ray / sphere intersection part of the blog, where we will explain the Phong shading algorithm used to shade the objects.
Visible Object creation process
The Simple Ray Tracer application, being at first hand an educational prototype, does not have a user friendly method of creating objects to be rendered: At this moment, any object must be declared in the main method and inserted into its appropriate ArrayList object. This is not difficult per say, and it is not the most convenient method, but, the intent being to demonstrate basic ray-tracing capabilities, it is sufficient:
Here is a code snippet creating a sphere of radius 0.4 world units located at [6, 1.5, 3.5] . We will explain the role of the other class members in the next blog chapter.
Sphere sphere2 = new Sphere(0.4);
VisibleObject class:
The VisibleObject class is an abstract super class from which the Sphere and Polygon class are derived. The VisibleObject class contains a center data member that can contain the center coordinate of a sphere instance. This abstract class also contains other data members, but those being related to object luminosity, colour and reflexive capabilities, these members will be best explained in the Ray / sphere intersection part of the blog, where we will explain the Phong shading algorithm used to shade the objects.
Visible Object creation process
The Simple Ray Tracer application, being at first hand an educational prototype, does not have a user friendly method of creating objects to be rendered: At this moment, any object must be declared in the main method and inserted into its appropriate ArrayList object. This is not difficult per say, and it is not the most convenient method, but, the intent being to demonstrate basic ray-tracing capabilities, it is sufficient:
Here is a code snippet creating a sphere of radius 0.4 world units located at [6, 1.5, 3.5] . We will explain the role of the other class members in the next blog chapter.
Sphere sphere2 = new Sphere(0.4);
sphere2.centre[0] = 6.0;
sphere2.centre[1] = 1.5;
sphere2.centre[2] = 3.5;
sphere2.alpha = 30.0;
sphere2.reflection_index = 1.0; // fully reflexive
sphere2.intensity_ambient[0] = 0.0;
sphere2.intensity_ambient[1] = 0.9;
sphere2.intensity_ambient[2] = 0.0;
sphere2.reflection_constant[0]= 0.3;
sphere2.reflection_constant[2]= 3.1;
sphere2.reflection_constant[1]= 3.1;
